Povray/tutorials/Loop

Introduction

Dans ce tutorial, je veux montrer quelques applications élémentaires de la boucle « tant que » [ While loops ] dans POV-Ray. La boucle While est employée pour le placement régulier des objets. Les exemples suivants montrent une boucle simple et des boucles imbriquées.

Fichiers inclus
Tous les fichiers de scène de POV-Ray des échantillons suivants sont téléchargeables. La plupart des fichiers de scène de POV-Ray emploient le fichier d'inclusion pour le système de coordonnées. Ce dernier a besoin d'un fichier de font.

Transformations linéaires

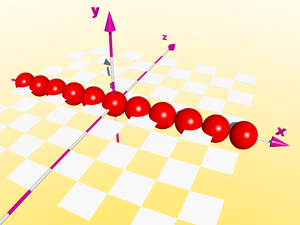
D'abord nous considérons une boucle simple qui place de petites sphères le long de l'axe de x, de x = -5 à x = +5 //------------------------------------ #declare Ball = sphere{<0,0,0>,0.5 texture{pigment{color Red} finish {ambient 0.15 diffuse 0.85 phong 1} } } #declare NrX = -5; // start #declare EndNrX = 5; // end #while (NrX < EndNrX+1) object{Ball translate <NrX,0,0>} #declare NrX = NrX + 1; //next Nr #end // ----------- fin de boucle ----

Simple boucle Fichier POVRay correspondant

Si nous imbriquons une boucle existante dans une autre boucle, faisant un pas de la valeur z = 0 à z = +5, nous obtenons un champ rectangulaire couvert par des objets identiques //------------------------------------ #declare Boxy = box {<0,0,0>,< 1,1,1> scale 0.5 texture{pigment{color White} finish {ambient 0.1 diffuse 0.9}}} #declare DistanceX = 1.00; #declare DistanceZ = 1.00; #declare NrX = 0; // startX #declare EndNrX = 7; // endX #while (NrX < EndNrX) // <-- loop X #declare NrZ = 0; // start #declare EndNrZ = 7; // end #while (NrZ < EndNrZ) // <- loop Z object{Boxy translate<NrX*DistanceX, 0, NrZ*DistanceZ>} #declare NrZ = NrZ + 1; // next NrZ #end // ------------- fin de boucle Z #declare NrX = NrX + 1;// next NrX #end // ----------- fin de boucle X --

Double boucle Fichier POVRay correspondant

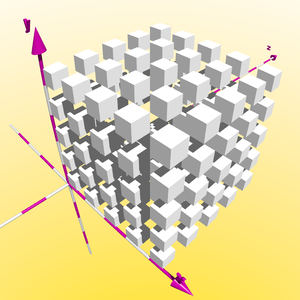
Il est posibble d'imbriquer une boucle dans une boucle additionnelle imbriquée, faisant un pas de la valeur y = 0 à y = +5. Avec ceci, nous obtenons une boîte constituée par les objets identiquement formés //------------------------------------ #declare DX = 1.00; #declare DY = 1.00; #declare DZ = 1.00; #declare NrX = 0; // startX #declare EndNrX = 5; // endX #while (NrX < EndNrX) #declare NrY = 0; // startY #declare EndNrY = 5; // endY #while (NrY < EndNrY) #declare NrZ = 0; // startZ #declare EndNrZ = 5; // endZ #while (NrZ < EndNrZ) object{Boxy translate <NrX*DX,NrY*DY,NrZ*DZ> } #declare NrZ = NrZ+1;// next NrZ #end // -------- fin de boucle Z #declare NrY = NrY+1;// next NrY #end // -------- fin de boucle Y #declare NrX = NrX+1;// next NrX #end // --------- fin de boucle X ----

Triple boucle Fichier POVRay correspondant

Avec cet échantillon, nos possibilités, considérée comme de pures transformations linéaires avec imbrication de boucles, nous semblons bien avoir parcouru tout notre monde tridimensionnel.

Transformations Circulaires

Jusqu'ici la boucle while a été seulement employée avec le mouvement de translation. Un effet intéressant résulte si nous employons le mouvement de rotation de la même manière. //---------------------------------- #declare Ball = sphere{<0,0,0>,0.6 texture{pigment{color Red} finish {ambient 0.15 diffuse 0.85 phong 1} } } #declare Radius = 3.00; #declare Nr = 0; // start #declare EndNr = 30; // end #while (Nr< EndNr) object{Ball translate<Radius,0,0> rotate<0,Nr*360/EndNr,0>} #declare Nr=Nr+1;//next Nr_minor #end // -------- fin de boucle ----

Simple boucle Fichier POVRay correspondant

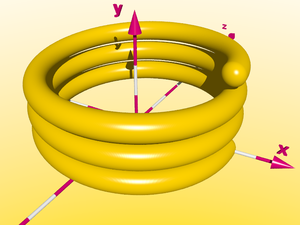
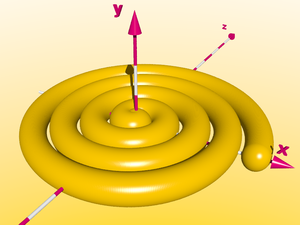
Si nous laissons en plus tourner les sphères autour de la direction de z, nous obtenons une spirale circulaire : //---------------------------------- #declare Ball = sphere{<0,0,0>,0.25 texture{..see above..}}} #declare R_major = 3.00; #declare R_minor = 1.00; #declare N_major = 10; #declare N_minor = 430; #declare Nr = 0; // start #declare EndNr=N_major*N_minor;// end #while (Nr < EndNr) object{Ball translate<R_minor,0,0> rotate<0,0,Nr * 360/N_minor> translate<R_major,0,0> rotate<0,Nr * 360/EndNr,0>} #declare Nr = Nr+1;//next Nr #end // ------ fin de boucle -------

Spirale Fichier POVRay correspondant

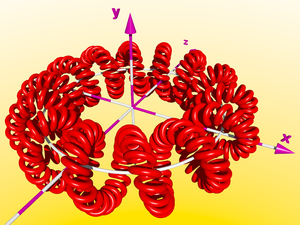
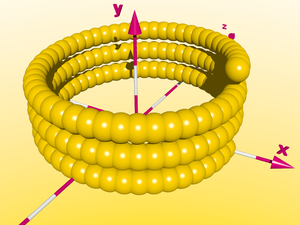
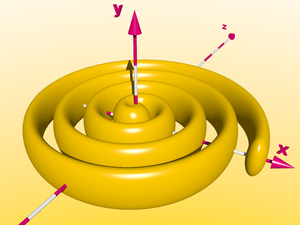
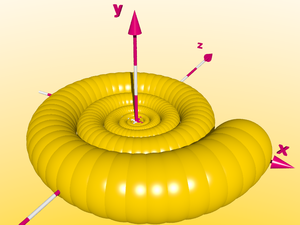
Si nous continuons ce petit jeu, nous obtenons une double spirale ciorculaire - le nombre de sphères devient énorme - dans le paysage suivant là sommes environ 25 000 boules sur le champ et environ 17 Mo de RAM ont été employées. #declare Ball = sphere{<0,0,0>,0.1 texture{.. see above..}}} //-------------------------------- #declare R_major = 3.50; #declare R_minor = 1.00; #declare R_inner = 0.30; #declare N_maj = 14; #declare N_min = 18; #declare N_in = 100; //-------------------------------- #declare Nr = 0; // start loop #while (Nr < N_maj*N_min*N_in) object{Ball translate<0,0,R_inner> rotate<0,Nr * 360/N_inner,0> translate<R_minor,0,0> rotate<0,0,Nr * 360/(N_min*N_in)> translate<R_major,0,0> rotate<0,Nr*360/(N_maj*N_min*N_in),0> } #declare Nr=Nr+1;// next Nr #end // --------- fin de boucle --

Double spirale Fichier POVRay correspondant

Moebius

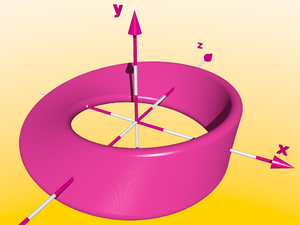
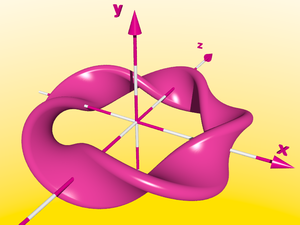
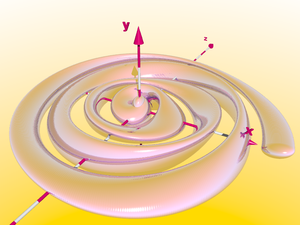
Si nous utilisons pour la double rotation un bâton, au lieu d'une sphère, comme élément de base, et ramenons le nombre de rotations intérieures à 0.5, nous obtenons un ruban de Möbius - ce genre de ruban a seulement un côté //--------------------------------- #declare P_R=0.2; #declare P_H=0.75; #declare Profile = union{ sphere {<0, P_H,0>,P_R} cylinder{<0,-P_H,0>,<0,P_H,0>,P_R} sphere {<0,-P_H,0>,P_R } texture{pigment{color rgb<1,.3,.7>} finish {ambient 0.45 diffuse 0.55 phong 1}}} //---------------------------------- #declare Radius_major = 3.00; #declare N_major = 0.5; #declare N_minor = 2000; //---------------------------------- #declare Nr =0; //start #declare EndNr=N_major*N_minor;//end #while (Nr< EndNr) object{Profile rotate<0,0,Nr * 360/N_minor> translate<Radius_major,0,0> rotate<0,Nr * 360/EndNr,0>} #declare Nr = Nr+1;// next Nr_minor #end // ---------- fin de boucle ----

Ruban de Moebius Fichier POVRay correspondant

Si nous changeons le nombre de rotations intérieures en 2.5, voici ce qui suit //---------------------------------- #declare N_major = 2.5; //----------------------------------

Rotation 2.5 Fichier POVRay correspondant

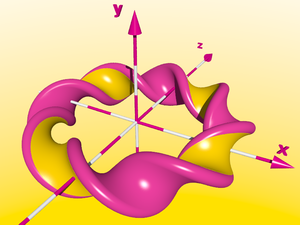
Dans le cas de rotations intérieures en nombre pair de demi-tours, nous avons des bandes avec 2 surfaces. C'est uniquement dans le cas de 0.5, 1.5, 2.5 rotations intérieures etc... que nous avons seulement 1 côté. //--------------------------------- #declare P_R = 0.2; #declare P_H = 0.65; #declare Profile = union{ sphere {<0, P_H,0>,P_R } cylinder{<0,-P_H,0>,<0,P_H,0>,P_R} cylinder{<0,-P_H,0>,<0,P_H,0>,P_R translate<0.01,0,0> texture{pigment{color rgb<1,.65,0>} finish {ambient 0.1 diffuse 0.9 phong 1}}} sphere {<0,-P_H,0>,P_R } texture{pigment{color rgb<1,0.3,0.7>} finish {ambient 0.45 diffuse 0.55 phong 1}}} //--------------------------------- #declare N_major = 4; //---------------------------------

Moebius à deux faces Fichier POVRay correspondant

Vis et spirales

La superposition de la rotation d'une sphère, et d'une translation le long de l'axe de cette rotation, donne une vis formée par l'emplacement de ces éléments //------------------------------------ #declare Ball = sphere {<0,0,0>,0.35 scale <1,1,1> texture{pigment{color rgb<1,0.8,0.2>} finish {ambient 0.1 diffuse 0.9 phong 1}}} #declare Radius = 3.00; #declare N_rev = 3;//NumberOFrevolution #declare N_p_rev=50;//ElementsPERrev. #declare H_p_rev=0.8;//Heightdiff./rev. #declare H = H_p_rev/N_p_rev; //----------------------------------- #declare Nr = 0; //start #declare EndNr = N_rev*N_p_rev;// end #while (Nr < EndNr) object{Ball translate<Radius,Nr*H,0> rotate<0,Nr*360/N_p_rev,0>} #declare Nr = Nr+1; // next Nr #end // ---------- fin de boucle -----

Vis avec 50 éléments par tour Fichier POVRay correspondant

Si nous augmentons le nombre d'éléments par révolution, ces éléments élémentaires se transforment dans une nouvelle forme. Le piège de cette technique : le nombre d'éléments et donc le besoin de RAM et de temps de calcul, qui augmentent très vite : ici nous avons 2000 sphères par révolution ! //------------------------------------ #declare N_p_rev=2000; //------------------------------------

Vis avec 2000 éléments par tour Fichier POVRay correspondant

Si nous ajoutons une translation radiale constante, en restant à hauteur nulle, nous obtenos une spirale //--------------------------------- #declare Ball = sphere {<0,0,0>,0.45 texture{pigment{color rgb<1,.8,.2>} finish {ambient 0.1 diffuse 0.9 phong 1}}} #declare Radius0 = 0.0; #declare N_rev = 4; #declare N_p_rev = 500; #declare D_p_rev = 1.0; #declare D = D_p_rev/N_p_rev; //-------------------------------- #declare Nr = 0; //start #declare EndNr=N_rev*N_p_rev;//end #while (Nr< EndNr) object{Ball translate<Radius0+Nr*D,0,0> rotate<0,Nr*360/N_p_rev,0> } #declare Nr = Nr + 1; // next Nr #end // ------- fin de boucle -----

Spirales Fichier POVRay correspondant

Spirales vrillées

Dans les derniers échantillons nous avons la plupart du temps employé des sphères. Si nous employons des ellipsoïdes à leur place, nous gagnons la possibilité de les tourner durant le déplacement, comme dans le Möebius. Tout d'abord une spirale avec ellipsoïdes //------------------------------------- #declare Ball = sphere{ <0,0,0>,0.45 scale <0.7,1.5,1> // !!! texture{ pigment{ color rgb<1,0.60,0.0>*0.7} finish {ambient 0.1 diffuse 0.65 phong 1}}} //le reste comme dans l'exemple précédent !

Spirales vrillées 1 Fichier POVRay correspondant

Maintenant, tournons cet ellipsoïde durant son trajet //------------------------------------ ... #while (Nr< EndNr) object{Ball rotate <0,0,Nr*0.5> // !!! translate<Radius0+Nr*D,0,0> rotate<0,Nr * 360/N_p_rev ,0>} #declare Nr = Nr+1; // next Nr ... //------------------------------------

Spirales vrillées 2 Fichier POVRay correspondant

Vrillons plus fort et voyons ce nous obtenons une nouvelle forme de vie étrange ? //------------------------------------ ... #while (Nr< EndNr) object{Ball rotate <0,0,Nr*3.5> // !!! translate<Radius0+Nr*D,0,0> rotate<0,Nr * 360/N_p_rev ,0>} #declare Nr = Nr+1; // next Nr ... //------------------------------------

Spirales vrillées 3 Fichier POVRay correspondant

Escargots et ammonites

Dans les derniers exemples de spirale, les sphères avaient toujours la même taille. Maintenant nous verrons comment réduire continuellement la taille des sphères, le rayon et la taille de la base du vissage, pour en faire un escargot //------------------------------------- #declare Ball = sphere{<0,0,0>,0.5 texture{pigment{color rgb<1,0.65,0.0>} finish {ambient 0.1 diffuse 0.9 phong 1}}} #declare Radius0=3.0;// basic radius #declare NR=9;//number of revolutions #declare NpR=100;//number elements p.r. #declare Scale=0.75; //per revolution #declare HpR=0.8;//difference in y p.r. //------------------------------------- #local Hd = HpR/NpR; #local Scale_p = pow(Scale,1/360); #local Scale_pE = pow(Scale_p,360/NpR); #local Old_S = Scale_pE; #local Old_H = Hd; #declare Nr = 0; //start #declare EndNr = NR*NpR; // end #while (Nr< EndNr) object{Ball translate<Radius0,0,0> scale Old_S translate<0,Old_H,0> rotate<0,Nr*360/NpR,0>} #declare Nr = Nr+1; // next Nr #declare Old_S =Scale_pE*Old_S; #declare Old_H =Old_H+Hd*Old_S; #end // ----------- fin de boucle -----

Coquille d'escargot Fichier POVRay correspondant

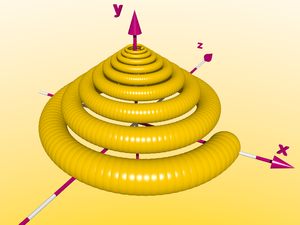
Si nous ramenons la hausse du vissage à zéro, nous obtenons la forme classique d'une ammonite //----------------------------------- #declare Ball = sphere{<0,0,0>,1.0 texture{...see above...}}} #declare Radius0 = 3.5; #declare NR = 9;//number of revolutions #declare NpR=50;//number of elem.p.r. #declare Scale = 0.55; //per revolution #declare HpR = 0.00; //------------------------------------

Ammonite Fichier POVRay correspondant

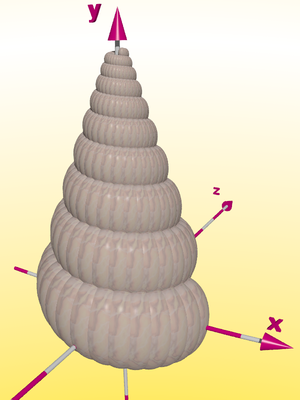
En mesurant la forme de l'élément de base et en lui donnant une consistance rugueuse avec des textures de pierre ou de granit il est possible de former presque chaque forme d'une coquille d'escargo ou d'ammonite que vous souhaitez : Par exemple : que diriez-vous d'un Turitella turis var. povensis ? //--------------------------------- #declare Ball = sphere{<0,0,0>,0.70 scale <1,1.5,1> texture{T_Stone3 scale 1.5 finish {ambient 0.2 diffuse 0.8 phong 0.3}}} #declare Radius0 = 1.5; #declare NR=9.1; //number of revolutions #declare NpR = 30; //number of elements per revolution #declare Scale=0.78; //per revolution #declare HpR = 1.6; //---------------------------------

Turitella turis var. povensis Fichier POVRay correspondant

Comparaison des boucles while et for

La boucle for est disponible depuis POV-Ray 3.7.

Mots réservés de POV-Ray
Pour éviter chaque collision avec des noms incorporés et des mots réservés de POV-Ray,

il est très recommandé d'utiliser seulement des mots qui commencent avec des capitals (lettres majuscules) pour tous les noms des variables declarés par l'utilisateur.

On doit tenir compte que x = <1,0,0> est un mot réservé, on prendra par ex. "X".

Syntaxe While Loop //------------------------------------ #local Identifier = Start; #while (Identifier <= End) //... do something // depending on value of Identifier. #local Identifier = Identifier + Step; #end // ------------- end of loop ---- Exemple 'While Loop' union{ //------------------------------- #local Cntr = 0; // start // while loop #while ( Cntr <= 5 ) object{ MyObject translate<0,0,Cntr*2> } // end of object #local Cntr = Cntr + 1; // next #end // -------- end of #while loop rotate<0,0,0> translate<0,0,0> } // end of union ----------------------

Syntaxe For Loop //------------------------------------ #for (Identifier, Start, End [, Step]) //... do something // depending on value of Identifier. #end // ------------- end of loop ---- Note: Step (longueur de pas) est optionnel ! (default Step=1) Exemple 'For Loop' union{ //----------------------------- //#for (Identifier, Start, End [, Step]) #for (Cntr, 0, 5, 1) object{ MyObject translate<0,0,Cntr*2> } // end of object #end // ----------- end of #for loop rotate<0,0,0> translate<0,0,0> } // end of union --------------------

Boucle infinie
On doit s'assurer que la boucle s'arrête vraiment après un nombre limité des pas ! Autrement POV-Ray fait le parsing d'une boulce sans fin et verser des données inutiles dans le RAM sans fin!